Конечные автоматы

Поведение многих объектов описывается так называемой конечно-автоматной моделью. В соответствии с этой моделью объект находится в одном из конечного множества состояний, а переходит в другое состояние под воздействием входных сигналов (команд, событий). Находясь в том или ином состоянии, объект вырабатывает некий выходной сигнал (параматр). Иначе говоря, конечный автомат — математическая (алгоритмическая) модель поведения устройств с конечной памятью. Конечные автоматы применяются, например, в системах синтаксического анализа и перевода текста, компьютерных играх, системах управления сложными техническими устройствами и др. Здесь рассматривается реализация конечного автомата на языке JavaScript на примере решения простой задачи смены картинок. Данный пример приведен не ради демонстрации преимуществ конечно-автоматной модели, а для иллюстрации логики последней.

Еще примеры применения конечных автоматов:

Светофор, управляемый конечным автоматом — статья на данном сайте.
Виджет посредством конечного автомата — статья на данном сайте.

Содержание

Что такое конечный автомат
Пример автомата Мура
Программная реализация автомата Мура
Программная реализация автомата Мили
Представление автоматами систем без памяти
Резюме

Что такое конечный автомат

Конечный автомат имеет конечное множество состояний. Под воздействием входных команд из некоторого конечного множества он может перейти в другое состояние и "выработать" некие значения выходных параметров.

Существуют несколько разновидностей конечного автомата. Здесь мы рассмотрим две из них — автомат Мура и автомат Мили.

В автомате Мура значения выходных параметров однозначно определяются состоянием, в котором он находится. При этом состояние, в которое он перейдет, однозначно определяется текущим состоянием и входной командой. Точнее, конечный автомат Мура характеризуется следующими пятью элементами:

С — конечное множество допустимых состояний;
X — конечное множество допустимых входных сигналов (команд);
Y — конечное множество допустимых выходных параметров (выходов);ˆ
trans(c,x) — функция переходов состояний, однозначно сопоставляющая любым допустимым состоянию и команде некоторое допустимое состояние;
out(c) — функция выходов, однозначно сопоставляющая любому допустимому состоянию некотрый допустимый выход.

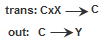Нередко к указанным пяти объектам добавляют еще начальное состояние автомата. Математически функции переходов и выходов записываются так:

,
где через x обозначена операция декартова произведения множеств С и X (это множество всевозможных пар состояние-команда).
Функция trans преобразует всевозможные пары (с,x) состояний-команд в состояния (элементы множества C); функция out преобразует любое состояние (элемент множества C) в некоторый выход (элемент множества Y).

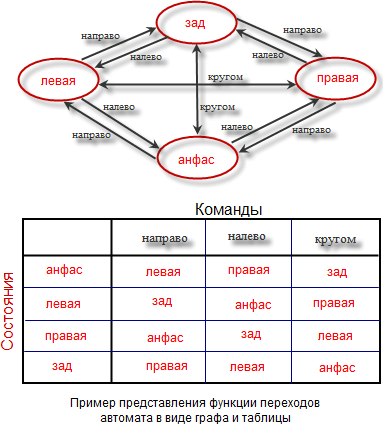
Функции переходов и выходов обычно представляют таблицами. При небольшом количестве состояний функцию переходов еще представляют в виде графа, вершинам которого соответствуют состояния автомата, а направленным дугам, помеченным командами, — собственно переходы.

Автомат Мили отличается от автомата Мура только функцией выхода, которая определена на множестве всех пар состояние-команда. Точнее, out(c,x) определяет выход автомата, который он будет иметь после подачи на него команды x, если при этом он находился в состоянии c. Любой конечный автомат Мили можно преобразовать в эквивалентный по поведению конечный автомат Мура, и наоборот.

Пример автомата Мура

Пусть, например, требуется, чтобы некий объект выполнял команды направо, налево и кругом, поворачиваясь в соответствующую сторону. Вид этого объекта в результате выполнения команды зависит не только от самой команды, но и от состояния объекта, в котором он нахдился.

Пусть состояние определяет, какой стороной объект обращен к нам: анфас, левая, правая, зад. Тогда функцию переходов состояний автомата, моделирующего указанное поведение, можно представить в виде графа или таблицы как показано на рисунке справа. Так, если объект находится в состоянии анфас, то при выполнении команды направо он должен показать нам свой левый бок, т.е. перейти в состояние левая. Если повторить ту же команду, то объект перейдет в состояние зад.

В рассматриваемом примере в качестве функции выхода автомата можно взять такую, которая сопоставляет каждому состоянию соответствующее графическое изображение объекта. Возможный вариант показан ниже. Вы можете выбрать команду, щелкнув на соответствующей кнопке, чтобы изменить положение автомобиля.

Автомобиль, повернись:

Программная реализация автомата Мура

Для реализации конечно-автоматной модели необходимо задать представления функций переходов и выходов состояний, а также "движок", который будет осуществлять эти переходы и выходы.

Функции переходов и выходов можно представить таблицами, а реализовать их программно — с помощью ассоциативных массивов, индексы которых представляются символьными строками, содержащими имена состояний и команд. Далее рассматривается, как это сделать.

Переходы состояний

Для рассмотренного примера функцию переходов состояний можно представить с помощью следующего массива:

var trans=[ ]; // массив переходов состояний автомата
trans['анфас']=[ ];
  trans['анфас']["направо"]="левая";
  trans["анфас"]["налево"]="правая";
  trans["анфас"]["кругом"]="зад";
trans['левая']=[ ];
  trans["левая"]["направо"]="зад";
  trans["левая"]["налево"]="анфас";
  trans["левая"]["кругом"]="правая";
trans['правая']=[ ];
  trans["правая"]["направо"]="анфас";
  trans["правая"]["налево"]="зад";
  trans["правая"]["кругом"]="левая";
trans['зад']=[ ];
  trans["зад"]["направо"]="правая";
  trans["зад"]["налево"]="левая";
  trans["зад"]["кругом"]="анфас";

Здесь первый индекс массива trans есть имя состояния, второй индекс — имя команды, а значение — имя состояния, в которое должен перейти автомат из состояния, указанного первым индексом, по команде, которая указана вторым индексом.

Выходы состояний

Функцию выходов автомата представим также в виде массива, элементами которого являются определения функций, изменяющих значение атрибута src элемента <img id='myimg' ...> (графического изображения):

var out=[ ]; // массив выходов автомата
  out["анфас"] =function() {document.getElementById('myimg').src="front.jpg"}
  out["левая"] =function() {document.getElementById('myimg').src="left.jpg"}
  out["правая"]=function() {document.getElementById('myimg').src="right.jpg"}
  out["зад"]   =function() {document.getElementById('myimg').src="back.jpg"}

Движок

Движок конечного автомата определим как объект automat, которому при инициализации передаются в качестве параметров массивы trans (переходов) и out (выходов), а также начальное состояние stat. Свойство stat автомата сохраняет имя текущего состояния. Метод input(команда) обеспечивает выдачу команды на вход автомата. Метод output() вычисляет выход автомата. Вот возможный вариант конструктора объекта automat:

function automat(trans,out,stat){ // движок автомата
  this.trans=trans; // массив переходов
  this.out=out;     // массив выходов
  this.stat=stat;   // текущее состояние
  this.input=function(inp){  // ввод команд
      if (inp){
        this.stat=this.trans[this.stat][inp];
        this.output=out[this.stat] // выход
      }
      return this.stat
  }
  this.output=out[this.stat];// выход
}

Ниже приведен скрипт, в котором создается экземпляр объекта automat с переходами trans и выходами out, установленный в начальное состояние "анфас". Затем выдается команда "налево" и вычисляется выход (в данном случае — функция для состояния "правая").

myautomat=new automat(trans,out,"анфас") // создание экземпляра объекта automat
myautomat.input("налево")                // выдача команды
myautomat.output()                       // вычисление выхода

На автомат можно подать последовательность из нескольких команд, а затем вычислить выход для конечного состояния. Например:

myautomat.input("налево");myautomat.input("налево");myautomat.input("налево");
myautomat.output()

На данной странице изображение автомобиля изменяется при щелчке на одной из трех кнопок. Вот соответствующий код:

<input type="button" value="направо"
       onclick="myautomat.input(this.value);myautomat.output()"/>
<input type="button" value="налево"
       onclick="myautomat.input(this.value);myautomat.output()"/>
<input type="button" value="кругом"
       onclick="myautomat.input(this.value);myautomat.output()"/>

Если требуется вычислять выходы при каждой выдаче команды, то вызов метода output() можно встроить в вызов метода input(), изменив код объекта automat, например, следующим образом:

function automat(trans,out,stat){ // движок автомата
  this.trans=trans; // массив переходов
  this.out=out;     // массив выходов
  this.stat=stat;   // текущее состояние
  this.input=function(inp){  // ввод команд
      if (inp){
        this.stat=this.trans[this.stat][inp];
        this.output=out[this.stat] // выход
        this.output();  // вычисление выхода
      }
      return this.stat
  }
  this.output=out[this.stat];// выход
  this.output();  // вычисление выхода
}

В данном случае можно не вызывать метод output() отдельно, поскольку он вызывается при выполнении метода input().

Программная реализация автомата Мили

Как уже отмечалось, автомат Мили отличается от автомата Мура функцией выхода. Автомат Мили генерирует выход в зависимости от текущего состояния и поданной на него команды. Далее приводятся определения выходов для рассматриваемого здесь примера с автомобилем, а также движка автомата Мили. Переходы (trans) такие же, что и для автомата Мура (см. выше). Методом input(команда) подается входная команда. При этом выход генерируется автоматически.

var front=function() {document.getElementById('myimg').src="front.jpg"};
var left=function()  {document.getElementById('myimg').src="left.jpg"};
var right=function() {document.getElementById('myimg').src="right.jpg"};
var back=function()  {document.getElementById('myimg').src="back.jpg"};

out=[]; // массив выходов автомата
out["анфас"]=[];
  out["анфас"]['направо']=left;
  out["анфас"]['налево']=right;
  out["анфас"]['кругом']=back;
out["левая"]=[];
  out["левая"]['направо']=back;
  out["левая"]['налево']=front;
  out["левая"]['кругом']=right;
out["правая"]=[];
  out["правая"]['направо']=front;
  out["правая"]['налево']=back;
  out["правая"]['кругом']=left;
out["зад"]=[];
  out["зад"]['направо']=right;
  out["зад"]['налево']=left;
  out["зад"]['кругом']=front;

function automat2(trans,out,stat){ // движок автомата Мили
  this.trans=trans; // массив переходов
  this.out=out;     // массив выходов
  this.stat=stat;   // текущее состояние
  this.input=function(inp){  // ввод команд
      if (inp){
        this.output=out[this.stat][inp] // выход
        this.output(); // вычисление выхода
        this.stat=this.trans[this.stat][inp];
       }
      return this.stat
  }
}

Представление автоматами систем без памяти

Системы без памяти (функциональные системы) характеризуются однозначной зависимостью выхода от входной команды. Автоматную модель такой системы можно представить как имеющую единственное состояние. В графе переходов такого автомата все дуги выходят из единственной вершины и замыкаются на ней, т.е. образуют петли. Такие модели удобно представлять как автоматы Мили.

Резюме

Вся информация о поведении объекта хранится в массивах trans и out. Вы можете изменять эти массивы в зависимости от конкретных задач или особенностей объекта управления. При этом реализация поведения объекта обеспечивается одним и тем же объектом — движком automat.

Предложенный в настоящей статье движок может быть, разумеется, доработан. Из возможных дополнений отметим лишь несколько самых важных:

Не помешает добавить обработку команд, которые соответствуют петлям графа переходов, а также вообще не предусмотренные для данного автомата. Такие команды не изменяют текущее состояние. Простейший вариант реализации этого состоит в небольшой модификации метода input:
```
  this.input=function(inp){  // ввод команд
      if (inp&&this.trans[this.stat][inp]){ ...}
    ...
  } 
  
```
В движок автомата можно добавить регистрацию обработчиков событий, на которые он должен реагировать как на команды. Например, для современных браузеров, отличных от IE 8 и более ранних версий, можно использовать стандартный метод
```
  htmlElement.addEventListener(событие, функция-обработчик, false)
  
```
Для IE 8 и более старых можно использовать метод
```
  htmlElement.attachEvent(событие, функция-обработчик)
  
```
Возможно, потребуются переменные и/или вспомогательные объекты для хранения промежуточных значений.

Содержание