Вадим Дунаев
О бесконечных множествах
Раздел из книги "Занимательная математика. Множества и отношения"
Профессор. Теория множеств создавалась как инструмент для выяснения устройства бесконечных совокупностей объектов. Бесконечность всегда привлекала внимание людей. Термином “бесконечность” сначала обозначали все, что было невозможно сосчитать или перечислить. Бесконечное — это что-то запредельное, невообразимо большое или, напротив, чрезвычайно малое, к чему можно стремиться сколь угодно долго, но достичь которого невозможно. Приведите, пожалуйста, пример бесконечного объекта.
Простак. Первое, что приходит мне на ум, — вселенная, состоящая из бесчисленного количества звезд, атомов и других частиц.
Зануда. Множество целых чисел бесконечно: какое бы число мы ни взяли, всегда можно перейти к следующему, прибавив к предыдущему 1. Таким образом, мы никогда не сможем сказать “вот, все целые числа перечислены и других целых чисел больше нет”.
Профессор. На каком
основании Вы, Простак, считаете вселенную бесконечной? В действительности Вы и
никто другой не знаете, какая она, — бесконечная или конечная. Муравью
килограммовый камень кажется бесконечно тяжелым. Число 2100
настолько огромно, что простой перебор всех целых чисел, не превышающих его, с
помощью самого современного компьютера потребует невообразимо много сроков
жизни самого компьютера. Тем не менее, количество таких чисел конечно. Это
означает, что процесс их пересчета когда-нибудь да закончится. Мы называем
вселенную бесконечной, имея в виду лишь ее очень большие размеры, а также то,
что никто из людей никогда не достигал ее границ. А вот множество всех целых
чисел в самом деле бесконечно. Иначе говоря, мы доподлинно знаем, что оно
бесконечно, поскольку таковым по определению оно создано нашим разумом. Для
обозначения бесконечно большого количества в математике используют специальный
символ 
, а
для бесконечно малого — 1/. Однако и 1/ это не числа, а просто символы, поскольку
они не подчиняется обычным правилам арифметики. Так, 2
, 100
, 
, т.е. арифметические
операции над бесконечно большим количеством оставляют это количество бесконечно
большим.
С античных времен бесконечное множество рассматривали как совокупность объектов, данную не в завершенном виде, а как постоянно формирующуюся. По заданному правилу эту совокупность можно было дополнить новыми объектами когда угодно. Так, множество целых чисел считалось существующим не актуально, в готовом или завершенном виде, а существующим только потенциально. Его можно было постоянно пополнять новыми членами, но этот процесс никогда не мог быть завершен. Такой взгляд на бесконечные множества существовал вплоть до начала 1870-х годов, когда Георг Кантор стал рассматривать бесконечные множества как данные актуально. В результате он показал, что одни бесконечные множества могут включать в себя другие, т.е. что бесконечные множества можно сравнивать в количественном отношении подобно конечным множествам.
Сравнение бесконечных множеств
Профессор. Конечные множества можно сравнить в количественном отношении (хотя бы принципиально, если не практически) так: сначала подсчитать количество элементов в каждом из них, а затем сравнить полученные числа. Для бесконечных множеств данный способ не годится, поскольку подсчет количества их элементов никогда не закончится или, лучше сказать, не завершится какими-то числами, которые можно сравнивать. Тем не менее, интуиция подсказывает нам, что одни из бесконечных множеств могут быть больше других. Попробуйте сравнить бесконечные множества всех натуральных и четных натуральных чисел.
Простак. Натуральные числа это 1, 2, 3, …. Каждое второе из них — четное. Очевидно, что четных чисел меньше в два раза, хотя и тех, и других бесконечно много.
Зануда. Странно все это. С одной стороны, оба множества бесконечны и не имеют количественной характеристики, а с другой — одно из них больше другого, и даже видно, во сколько раз.
Профессор. Похоже, вы оба согласны, что бесконечные множества можно сравнивать. Однако результат сравнения, полученный Простаком, оказался неверным. В действительности четных натуральных чисел столько же, сколько и всех натуральных чисел. Прежде чем разобраться с этой задачей, попробуйте решить более простую. Пусть имеются конечные множества болтов и гаек. Как определить без подсчета, равны ли их количества?
Простак. Я бы стал навинчивать гайки на болты или просто выкладывать пары болт-гайка. Если бы для каждого болта нашлась бы своя гайка, то количества болтов и гаек равны, а в противном случае — нет. Таким образом, я решил задачу, не выясняя, сколько именно было гаек и болтов.
Профессор. Прекрасно. Воспользуемся Вашим методом применительно к бесконечным множествам чисел.
Простак. Идея метода состоит в сопоставлении друг другу элементов различных множеств. Выпишем ряд натуральных чисел, а под ним — ряд натуральных четных чисел:
1, 2 , 3, 4, 5, 6, … — натуральные числа;
2, 4, 6, 8, 10, 12, … — четные натуральные числа.
Не трудно заметить, что каждому натуральному числу однозначно соответствует некоторое четное натуральное число. Так, натуральному числу n соответствует четное натуральное число 2n. И наоборот, каждому четному натуральному числу k однозначно соответствует натуральное число k/2. Выходит, можно образовать пары из элементов рассматриваемых множеств так, что ни один элемент какого-то из двух множеств не окажется без пары. Следовательно, множества натуральных и четных натуральных чисел равночисленны, если позволительно так сказать.
Профессор. Вы прекрасно справились с данной задачей. Поскольку количество элементов бесконечного множества не может быть выражено каким-либо числом, то говорят не о количестве, а о мощности множества. Для конечных множеств понятия их количества и мощности совпадают. Итак, только что установлено, что множества всех натуральных чисел и четных натуральных чисел равномощны. Очевидно, что аналогичным способом можно доказать, что равномощны множества натуральных и нечетных натуральных чисел.
Зануда. Я вынужден согласиться с приведенным доказательством равномощности рассматриваемых множеств, хотя результат не согласуется с интуицией, которая говорит нам, что множество натуральных чисел состоит из четных и нечетных натуральных чисел, взятых вместе. Таким образом, мы видим, что нарушается принцип, что целое больше своей части.
Профессор. Это один из примеров того, что иногда математика позволяет выяснить нечто, не подвластное нашей интуиции. Соотношения, выполняющиеся для конечных множеств, могут не выполняться применительно к бесконечным множествам. Бесконечность имеет особые свойства, которых нет в конечном. Так в чем же состоит метод, с помощью которого мы устанавливаем равномощность или неравномощность множеств?
Зануда. Как мы видели, суть метода состоит в попытке установить соответствие между элементами сравниваемых множеств. Это соответствие должно быть взаимно однозначным, чтобы множества были равномощными. Иначе говоря, каждому элементу одного множества должен соответствовать некоторый единственный элемент другого множества, и наоборот.
Профессор. Вы верно выразили суть метода сравнения множеств по их мощности. Теперь вы сможете сравнить множества натуральных и целых чисел. Попробуйте сделать это.
Простак. Целые числа это натуральные числа плюс те же
натуральные числа, но со знаком “минус”, и еще 0. Иначе говоря, целые числа
можно представить рядом: …-3, -2, -1, 0, 1, 2,
3, …. Очевидно, что множество целых
чисел содержит в качестве своего подмножества все натуральные числа. Однако это
еще не основание говорить о том, что данные множества неравномощны. Попробуем
установить взаимно однозначное соответствие между ними, для чего выпишем ряды
чисел один под другим:
… -3, -2, -1, 0, 1, 2, 3, …
… 1, 2, 3,…
Однако из данной записи не очевидно, как следует образовывать пары чисел из двух рядов и возможно ли это в принципе. Здесь надо подумать.
Зануда. Давайте упорядочим целые числа иначе: 0, 1, -1, 2, -2, 3, -3, …; натуральные числа оставим в их естественном порядке. Расположим ряды этих чисел один под другим:
0, 1, -1, 2, -2, 3, -3, …— целые числа;
1, 2, 3, 4, 5, 6, 7, … — натуральные числа.
Нетрудно заметить, что n-е по порядку целое число (обозначим его через zn) можно вычислить по следующей формуле:
zn = n/2, если n четное;
zn = - (n-1)/2, если n нечетное.
С другой стороны, для каждого целого числа z можно однозначно указать его номер (натуральное число):
n= 2z, если z > 0;
n = 2z+1, если z
0.
Таким образом, между целыми и натуральными числами установлено взаимно однозначное соответствие: каждому натуральному числу однозначно сопоставляется некоторое единственное целое число и, наоборот, каждому целому числу однозначно соответствует некоторое единственное натуральное число. Следовательно, натуральных чисел не меньше, но и не больше, чем целых, а значит их множества равномощны.
Профессор. Хорошее решение, приводящее к правильному результату.
Итак, мы только что убедились, что множества всех натуральных, только четных натуральных, только нечетных натуральных и целых чисел равномощны. При этом равномощность множеств определяется как существование взаимно однозначного соответствия между элементами данных множеств. Замечу, что кажущаяся парадоксальность полученных результатов имеет своей причиной рассмотрение бесконечных множеств как актуально данных в своем завершенном виде. Такой подход к бесконечным множествам был выполнен Кантором преднамеренно, хотя еще Галилео Галлией указывал, что он приведет к необходимости признать, что четных чисел столько же, сколько четных и нечетных вместе, а это по мнению подавляющего большинства его современников и предшественников считалось абсурдным.
Для бесконечных множеств такое утверждение, как “часть меньше целого” перестает быть верным. Это заметил еще древнегреческий математик Зенон, рассматривая следующее обстоятельство. Пусть дан треугольник АВС, в котором отрезок В’C’ параллелен основанию ВС и соединяет середины сторон, выходящих из вершины А. Спроектируем из этой вершины на ВС все точки отрезка В’C’. Тогда каждой точке отрезка В’C’ будет соответствовать некоторая точка основания ВС и, наоборот, каждой точке основания треугольника будет соответствовать какая-то точка отрезка В’C’. Например, точке X’ будет соответствовать точка X, а точке X — точка X ’. Следовательно, на отрезке В’C’, параллельном и равном отрезку ВА’ (А’ — середина основания ВС), размещается столько же точек, сколько и на вдвое большем отрезке ВС. При этом Зенон не знал, что аналогичный парадокс возникает при сравнении бесконечных подмножеств множества целых чисел.
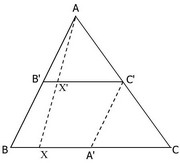
На отрезке В’C’ размещается столько же точек, сколько на вдвое большем отрезке ВС
А теперь рассмотрим множество рациональных чисел, т.е. целых и дробей. Рациональное число, как известно, можно представить как частное от деления двух целых чисел. Особенность множества рациональных чисел состоит в том, что между любыми соседними целыми числами находится бесконечно много рациональных чисел. Например, между 0 и 1 находятся дроби 1/2, 1/3, 1/4, 1/5, … . Возникает подозрение, что рациональных чисел больше, чем целых: целых бесконечно много, а между любыми соседними целыми находится тоже бесконечно много чисел. Получается бесконечное множество, составленное из бесконечных множеств, что, согласитесь, представляется более сложным, чем множество натуральных чисел. Однако, как показал Кантор в 1874г., рациональных чисел столько же, сколько и натуральных. Трудность, с которой он столкнулся, заключалась в поиске способа нумерации рациональных чисел. Кантор расположил рациональные числа не в один ряд, а в бесконечной квадратной таблице, т.е. в бесконечно много рядов. Далее оставалось только найти зигзагообразный путь обхода всех чисел, позволяющий последовательно пронумеровать каждое из них.
Всякое множество, элементы которого можно взаимно однозначно сопоставить натуральным числам, Кантор назвал счетным. Другими словами, элементы счетного множества можно пересчитывать.
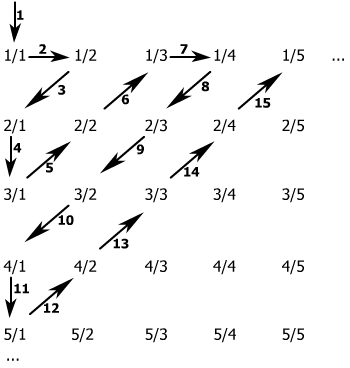
Метод доказательства счетности рациональных чисел
Зануда. А существуют ли несчетные множества, элементы которых пересчитать нельзя?
Профессор. Да, существуют. Например, множество всех
действительных чисел, содержащее кроме рациональных еще и иррациональные числа
(например, 
,
),
несчетно. Множество действительных чисел находится во взаимно однозначном
соответствии с множеством точек прямой. Обратите внимание, что множество
рациональных чисел значительно “плотнее” множества целых чисел (между любыми
соседними целыми числами располагается бесконечное множество рациональных
чисел), но тем не менее оба эти множества равномощны. Плотность же множества
действительных чисел существенно больше, и пересчитывать их нельзя. Последнее
означает, что не существует взаимно однозначного соответствия между множествами
действительных и натуральных чисел.
Простак. Мне трудно поверить в это. Что же может помешать нам последовательно, без пропусков, перебирать действительные числа, приписывая им натуральные номера?
Зануда. Сначала всем нам было трудно поверить, что натуральных чисел столько же, сколько целых и даже рациональных, а теперь трудно поверить, что есть множество, для нумерации элементов которого натуральных чисел просто не хватит. Но ведь именно последнее лучше всего согласуется с нашей интуицией. Воистину, наш разум способен сначала из сложного сделать простое, чтобы потом снова все усложнить! Вы хотите сказать, профессор, что нельзя придумать способ нумерации действительных чисел?
Профессор. Именно так!. Рассмотрим идею доказательства этого утверждения, придуманного Кантором. Сначала он предположил, что взаимно однозначное соответствие между натуральными и действительными числами существует. Затем он показал, что данное предположение приводит к противоречию и, следовательно, взаимно однозначное соответствие между натуральными и действительными числами невозможно. Таким образом, Кантор использовал метод доказательства от противного.
Доказательство можно заметно упростить, рассматривая только подмножество всех действительных чисел, заключенных между 0 и 1. Если уж это бесконечное подмножество окажется больше множества всех натуральных чисел, то все множество действительных чисел и подавно больше его.
Итак, предположим, что действительные числа в промежутке между 0 и 1 могут быть пронумерованы без повторов и пропусков натуральными числами. Другими словами, мы допускаем гипотезу, что все действительные числа, расположенные между 0 и 1, могут быть поставлены во взаимно однозначное соответствие с множеством натуральных чисел. Это означает, что мы можем составить некий бесконечный перечень действительных чисел, каждое из которых можно представить в виде бесконечной десятичной дроби.
Всякое действительное число можно представить бесконечной десятичной дробью. Такие бесконечные десятичные дроби, как 0.5000…, представим в виде эквивалентной бесконечной дроби 0.4999…. Перечень всех десятичных дробей, представляющих все действительные числа в промежутке от 0 до 1, может быть любым с точки зрения их порядка. Просто представим мысленно этот список: бесконечное количество различных бесконечно длинных десятичных представлений действительных чисел от 0 до 1. Каким бы ни был этот список, пронумеруем его элементами натуральными числами без пропусков и повторений. Перечень или, другими словами, список это — последовательность элементов, которым можно сопоставить натуральные числа: первому в списке элементу сопоставим 1, второму — 2 и т.д.
Теперь задача состоит в том, чтобы построить такую десятичную дробь, которой нет в указанном списке. Если нам это удастся, то тем самым мы докажем, что наш первоначальный перечень всех действительных чисел от 0 до 1 не полон и, следовательно, его нумерация не является нумерацией всех десятичных дробей от 0 до 1. Разумеется, мы можем пополнить начальный перечень вновь сконструированным числом. Однако ничто не мешает нам повторить аналогичные рассуждения, с помощью которых мы создадим еще одно новое действительное число, которого раньше не было в списке, и так далее. Итог будет один — список нумерованных действительных чисел всегда не полон. А это означает, что наша нумерация относится не к тому объекту, для которого она предназначалась изначально. Иначе говоря, наша нумерация нумерует не все действительные числа от 0 до 1 и, следовательно, она не является нумерацией этого подмножества действительных чисел. Так как это положение вещей будет сохраняться при сколь угодно долгом пополнении первоначального списка вновь созданными действительными числами, то мы должны признать, согласно Кантору, что нумерации действительных чисел просто не существует. Такова идея доказательства.
Зануда. Уважаемый профессор, если я Вас правильно понял, получается следующее. Сначала мы предполагаем, что множество действительных чисел можно представить в виде перечня всех его элементов, пусть даже бесконечного. Само понятие перечня предполагает некоторую, хотя бы произвольную, упорядоченность его элементов. Так, перечень создается из элементов любого множества следующим образом: сначала как-то выбирается первый элемент, затем второй и, далее, все остальные. Коль скоро мы можем сделать это, то можем и пронумеровать элементы этого списка натуральными числами 1, 2, 3,… . Таким образом, гипотеза о возможности нумерации действительных чисел уже провозглашена. Далее Вы, профессор, вместе с Кантором, говорите, что любая нумерация этого множества таковой не является по той простой причине, что само множество не соответствует своему определению, т.е. не является множеством всех действительных чисел в промежутке от 0 до 1. Ведь Вы говорите, что можете построить число, не входящее в исходный перечень. На этом основании Вы заключаете, что нумерация действительных чисел невозможна.
Профессор. Вы верно поняли мысль Кантора, которую я намерен лишь только растолковать, не претендуя ни на что большее. Давайте теперь рассмотрим ее техническую сторону. Это интересно как феномен изобретательской деятельности человека.
Итак, мы должны построить новое число, которого не было в первоначальном списке. Это число должно отличаться по крайней мере одним десятичным знаком (цифрой в одном из разрядов) от каждого из действительных чисел в списке. Вместе с тем, оно должно быть действительным числом, расположенным между 0 и 1.
Пусть имеется бесконечный перечень бесконечных десятичных представлений действительных чисел от 0 до 1. В этом перечне такие бесконечные десятичные дроби, как 0.5000…, представим в виде эквивалентной бесконечной дроби 0.4999….. Для построения нового числа, не входящего в указанный перечень, выполним следующие действия:
1. Берем первое число в исходном перечне. Первую десятичную цифру в новом числе определяем так:
· Если первая цифра десятичного представления рассматриваемого числа из перечня равна 1, то пишем 9 на первом месте после разделительной точки;
· Если первая цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на первом месте после разделительной точки.
2. Берем второе число в исходном перечне и определяем вторую цифру в новом числе:
· Если вторая цифра десятичного представления рассматриваемого числа равна 1, то пишем 9 на первом месте после разделительной точки;
· Если вторая цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на втором месте после разделительной точки.
3. Построение нового числа продолжается путем изменения n-ой цифры n-го числа в исходном списке аналогичным образом:
· Если n-я цифра десятичного представления рассматриваемого числа равна 1, то пишем 9 на n-м месте после разделительной точки;
· Если n-я цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на n-м месте после разделительной точки.
Новое число будет отличаться по крайней мере одним десятичным знаком от каждого действительного числа в исходном перечне и, вместе с тем, оно будет действительным числом, расположенным в промежутке от 0 до 1. Таким образом, предположение, что действительные числа можно взаимно однозначно сопоставить с натуральными числами, приводит к противоречию, а потому должно быть отброшено. Обратите внимание, что при доказательстве мы просматривали цифры чисел в перечне по диагонали. Поэтому метод, которым был получен данный результат, называют диагональным.
Диагональный метод доказательства того, что множество действительных чисел несчетно
Множество всех подмножеств данного множества
Профессор. Ранее мы рассматривали операции
(объединение, пересечение, вычитание), с помощью которых можно было из одних
множеств получать другие множества (см. разд. 3.2). Новые множества могут быть построены
и другими средствами. Так, мы можем рассмотреть множество, составленное из всех
подмножеств данного множества. Пусть, например, дано множество 
из трех элементов.
Тогда множество всех его подмножеств (обозначим его как 
) состоит из восьми
элементов:
={
— само множество 
,
Ø — пустое
множество
}
Обратите внимание, что элементами множества являются множества.
Если множество состоит
из n элементов, то множество всех его
подмножеств состоит из 
элементов. Если обозначить количество
элементов множества как ||, то
. В частности
пустое множество не имеет элементов (|Ø|=0), поэтому 
. Я надеюсь, что вы
понимаете, в чем состоит различие между и 
.
Очевидно, что множество всех подмножеств конечного
множества всегда больше данного множества: 
. А выполняется ли это неравенство в
случае бесконечных множеств?
Зануда. Сразу и не скажешь. Надо проверить,
возможно ли взаимно однозначное соответствие между множествами и . Но как его
построить?
Простак. Но быть может следует попытаться доказать
неравенство методом
от противного, чтобы не заниматься взаимно однозначным соответствием в явной
форме?
Профессор. Это хорошая идея. Попробуйте реализовать ее.
Простак. Пусть это сделает Зануда со всей присущей ему тщательностью.
Зануда. Хорошо, я попытаюсь. Итак, теорему
сформулируем следующим образом: любое множество неравномощно множеству всех его
подмножеств.
Доказывать будем методом от противного, т.е. предположим,
что равномощно
множеству .
Но это означает, что существует взаимно однозначное соответствие между элементами
множества и
элементами множества . Здесь я позволю себе ввести несложные
символические обозначения. Пусть 
— указанное взаимно однозначное
соответствие; 
—
подмножество множества , которое соответствие 
сопоставляет
элементу 
.
Надеюсь понятно, что 
.
Очевидно, что каким бы ни было взаимно однозначное
соответствие ,
для любого элемента 
возможны два варианта:
q
—
элемент принадлежит сопоставляемому множеству;
q
—
элемент не принадлежит сопоставляемому множеству
Вот здесь начинается самое интересное. Рассмотрим
подмножество 
множества
всех тех
элементов ,
для которых .
Не исключено, что множество пусто, но это не имеет значения. Так
как соответствие взаимно
однозначно, то существует элемент , для которого 
. Спрашивается, что имеет
место: 
или
?
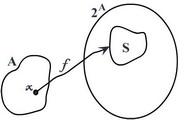
Соответствие f cопоставляет элементу x множества А некоторое его подмножество S
Допустим сначала, что . Но тогда , а и, следовательно, . Получаем
противоречие. Предположим обратное: . Но тогда 
и опять получаем
противоречие. Другими словами, с одной стороны , а с другой — . Данное противоречие мы
получили в предположении, что множества и равномощны. Отсюда следует, что
предположение было неверным. Значит, множества и не равномощны. На этом доказательство
заканчивается.
Простак. Как только Зануда ввел в рассмотрение
подмножество из
всех таких элементов, что , я сразу понял, что следует ожидать
противоречия. Это подмножество определяется таким же способом, как и множество
гетерологических прилагательных, или множество тех, кого должен брить
брадобрей. Только в данном случае противоречивость такого множества сыграла нам
наруку, а не просто обескуражило.
Профессор. Как мы уже знаем, множества натуральных, целых и рациональных чисел счетны, а множество действительных чисел — нет. Теперь мы узнали, что множество всех подмножеств данного множества больше последнего. Например, множество всех подмножеств натуральных чисел больше множества всех рациональных чисел.
Прямая и плоскость
Профессор. Мы знаем со времен Рене Декарта, привнесшего числа и алгебру в геометрию, что каждой точке прямой можно сопоставить число — координату этой точки. Пусть дан отрезок прямой, левому концу которого приписано число 0, а правому — 1. Внутренним точкам данного отрезка взаимно однозначно сопоставлены числа в промежутке от 0 до 1 в их естественном порядке. Но какие числа? Хватит ли для этой цели только рациональных чисел (т.е. дробей)?
Простак. Любой отрезок прямой состоит и бесконечного количества точек. Точка не имеет протяженности. Если бы мы взяли лишь конечное их количество на отрезке прямой, то между ними образовались бы промежутки. С увеличением количества точек ширина промежутков между ними уменьшалась бы, но оставаясь все же больше нуля. Но тогда возможен случай, когда два отрезка пересекаются не в точке а в промежутке, что противоречит аксиоме евклидовой геометрии, согласно которой две пересекающиеся прямые имеют одну и только одну общую точку.
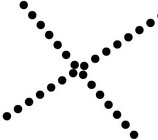
При недостаточной плотности точек пересекающиеся отрезки могут не иметь общей точки
Зануда. То, что точек в отрезке конечной длины бесконечно много, и так понятно.
Простак. А я и не собирался это доказывать. Просто я хотел наглядно показать, что может быть, если множество точек не достаточно плотно.
Зануда. Физическая линия как след, оставленный карандашом, под лупой с достаточным увеличением предстанет как набор дискретных пятен. Математическая же линия и под микроскопом любой силы будет выглядеть так же, как и без него. Впрочем, математическую линию мы видим не глазами, а умом. Плотность точек на ней столь велика, что между ними нет никаких промежутков. Не пойму, куда ты клонишь?
Простак. Минуточку терпения, Зануда. Допустим
теперь, что каждой точке отрезка прямой можно взаимно однозначно сопоставить
рациональные числа из подмножества, например, от 0 до 1. Возьмем два таких
отрезка и используем их в качестве катетов прямоугольного треугольника. Заметьте,
что концевые точки гипотенузы являются одновременно и концевыми точками
катетов, на которые гипотенуза опирается. Другими словами, вершины треугольника
это общие точки гипотенузы и смежных с ней катетов. Мы не можем удалить
концевую точку ни гипотенузы, ни катета, ибо вершина треугольника это по
определению точка пересечения сторон треугольника. Длины катетов равны 1, а
гипотенуза, согласно теореме Пифагора, имеет длину . Это число, сопоставленное
концевой точке гипотенузы не является рациональным, т.е. оно не может
быть получено делением одного целого числа на другое целое число. Следовательно,
рациональных чисел недостаточно, чтобы их можно было поставить во взаимно
однозначное соответствие с точками отрезка прямой.
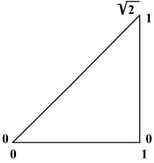
Рациональных чисел недостаточно, чтобы их можно было поставить во взаимно однозначное соответствие с точками отрезка прямой
Профессор. Будем считать Ваши рассуждения, Простак, не строгим доказательством, а проясняющими существо дела. Итак, точек на прямой больше, чем рациональных чисел. В действительности их столько же, сколько действительных чисел — рациональных и иррациональных вместе взятых. Это означает, что меду этими двумя множествами существует взаимно однозначное соответствие.
Говорят, что множества точек прямой (вообще любой линии) и действительных чисел образуют континуум — бесконечную и непрерывную совокупность. Между любыми двумя сколь угодно близкими точками линии находится бесконечно много точек, а между любыми двумя действительными числами находится бесконечно много действительных чисел.
А что вы скажете о возможности взаимно однозначного соответствия между множествами всех точек прямой и плоскости, например, между точками отрезка единичной длины и квадрата со стороной, равной 1?
Простак. Мне кажется, что в данном случае взаимно однозначного соответствия быть не может, поскольку точек в квадрате явно больше, чем на прямой. Можно представить себе квадрат как бесконечно много отрезков параллельных прямых, расположенных одна подле другой и покрывающих всю его площадь. При этом мощность множества таких отрезков должна быть такой же, как и мощность множества точек любого из них. А эта мощность, как нам уже известно, равна мощности множества всех действительных чисел.
Зануда. Ааналогия с покрытием квадрата очень узкими полосами лишь делает наглядными трудности построения или хотя бы выяснения возможности взаимно однозначного соответствия между точками квадрата и отрезка прямой. Интуиция подсказывает мне, что Простак скорее прав, чем не прав. Однако, имея дело с бесконечными множествами, мы должны быть готовы ко всему.
Профессор. Оказывается точки квадрата можно
отобразить на точки отрезка прямой взаимно однозначным образом. Когда Кантор
доказал это в 1877г., то сам был чрезвычайно удивлен полученным результатом: “Я
вижу это, но никак не могу этому поверить!” Для большинства математиков это
было настоящей сенсацией, а немецкий математик Л. Кронекер вообще не принял его. Кронекер известен очень высокими требованиями к строгости определений математических
объектов. Считая, что “Бог создал целые числа, а все остальное — дело рук
человеческих”, он, в частности, не признавал существования иррациональных
чисел. Так, число он
представлял бесконечной суммой рациональных чисел 1 –
1/3 + 13 – 1/7 +...
Я лишь кратко поясню идею
доказательства Кантора возможности взаимно однозначного соответствия между
точками плоскости и прямой. Каждая точка плоскости представляется парой чисел —
координатами 
,
которые можно представить бесконечными десятичными дробями. Эти две дроби
комбинируются по определенному правилу, чтобы получить одну дробь, которая
сопоставляется с точкой на прямой. Данная процедура обратима и, следовательно,
она устанавливает взаимно однозначное соответствие между точками плоскости и
прямой.
Комбинация двух десятичных
дробей, представляющих точку на плоскости, производится следующим образом.
Цифры дроби последовательно разбиваются на группы. Каждая цифра, кроме 0,
начинает новую группу. Бесконечная дробь, соответствующая точке на прямой,
составляется из полученных групп цифр: первая группа из числа , первая группа из
числе 
, вторая
группа из числа ,
вторая группа из числа и так далее.
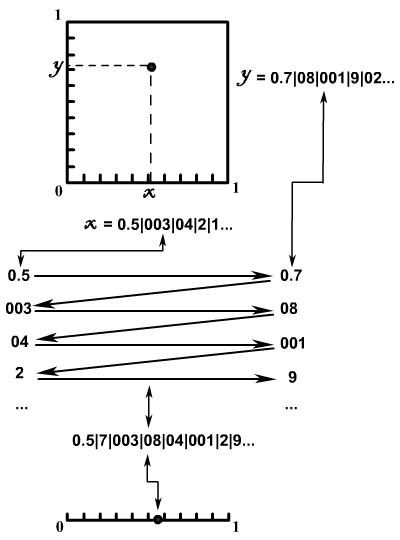
Установка взаимно однозначного соответствия между точками плоскости и прямой
Парадоксы бесконечности
Рука дающего не оскудеет
Профессор. Представим себе мешок с бесконечным количеством шаров, пронумерованных натуральными числами. В течение одной минуты шары вынимаются из мешка и возвращаются обратно по следующему алгоритму:
1. За одну минуту до окончания данного алгоритма из мешка вынимается шар с номером 1.
2. Через 1/2 минуты после шага 1 из мешка вынимаются шары с номерами 2 и 3, а шар 1 возвращается в мешок.
3. Через 1/4 минуты после шага 2 из мешка вынимаются шары с номерами 4, 5, 6, 7, а шары 2 и 3 возвращаются.
4. Через 1/8 минуты после шага 3 из мешка вынимаются шары с номерами 8, 9,…, 15, а шары 4, 5,6, 7 возвращаются. Следующие шаги данного алгоритма выполняются аналогичным образом.
Не трудно заметить, что в каждый момент из мешка извлекается в два раза больше шаров, чем возвращается назад. Сколько шаров окажется вне мешка ровно через минуту после начала работы описанного алгоритма?
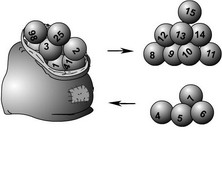
В каждый момент из мешка извлекается вдвое больше шаров, чем возвращается обратно
Зануда. На первом шагу, в самом начале минуты, вне мешка был один шар. На втором шагу, через 1/2 минуты, — 2 шара, на третьем, еще через 1/4 минуты, — 4 шара. На n-м шагу, через 1/2n-1 минуты после предыдущего шага или за это же время до окончания минутного срока, вне мешка будет 2n-1 шара.
Очевидно, что необходимо сначала определить, сколько шагов будет сделано в течение всей минуты. Первый шаг был сделан в начале минуты, второй — через 1/2 (т.е. 1/21 ) минуты, третий — через 1/21 + 1/22 после начала, четвертый — через 1/21 + 1/22 + 1/23, n-й шаг был сделан через 1/21 + 1/22 + 1/23 + … + 1/2n-1 минуты. Очевидно, что количество шагов n, выполненное за одну минуту, можно найти из уравнения:
1/21 + 1/22 + 1/23 + … + 1/2n-1 = 1
Правда, я не знаю, как его решить, но это, я думаю, трудность технического характера, которую можно преодолеть с помощью, например, математического справочника.
Простак. Давайте попробуем составить другое уравнение. А именно, попытаемся определить, сколько времени еще осталось до истечения минуты на n-м шаге алгоритма. На первом шаге остается еще целая минута, на втором — 1/2 = 1/21 минуты, т.к. этот шаг был сделан через полминуты после начала работы. На третьем шаге оставалось 1/4 = 1/22 минуты, а на n-м шаге — 1/2n-1 минуты. Чтобы определить номер шага, на котором минута будет полностью исчерпана, достаточно решить очень простое уравнение:
1/2n-1 = 0
Теперь мы хорошо видим, что ни при каком конечном числе n это равенство не выполняется точно, но в то же время замечаем, что с ростом n левая его часть очень быстро приближается к 0. Можно сказать, что при n→∞ величина 1/2n-1 равна нулю со сколь угодно большой точностью. Например, на 10-м шаге работы алгоритма до окончания минуты останется меньше 0.12 секунды, а на 25-м шаге — меньше 0.000004 секунды. Это я подсчитал с помощью калькулятора.
Зануда. Но, насколько я помню, в задаче спрашивалось, сколько шаров окажется вне мешка ровно через минуту. На n-м шаге работы алгоритма это количество, как мы уже видели, равно 2n-1. Минута будет исчерпана при n→∞ и, следовательно, вне мешка окажется бесконечно много шаров.
Простак. Но ведь и в мешке будет также бесконечно много шаров.
Зануда. А почему это тебя удивляет? Нас же теперь не шокирует тот факт, что если из множества всех целых чисел удалить все только четные числа, коих бесконечно много, то оставшихся чисел также будет бесконечно много.
Простак. Я не это имел ввиду, просто неудачно выразился. Меня удивляет, что по истечении минуты любой конкретный шар окажется в мешке, не смотря на то, что вне мешка будет бесконечно много шаров. Например, где окажется k-й шар в момент истечения минуты?
В момент, сколь угодно близкий к завершению минуты, шары 1, 2, 3 и так далее до, возможно, какого-то k-го шара уже будут в мешке. Особым является момент извлечения-возвращения шаров. Рассмотрим его подробнее.
Можно заметить, что на n-м шаге работы алгоритма из мешка извлекаются шары с номерами:
2n, 2n + 1, …, 2n+1 -1,
а назад возвращаются (если n >1) шары с номерами:
2n-1, 2n-1 + 1, …, 2n - 1.
Для любого номера k найдется шаг n алгоритма такой, что
2n-1 k 2n -
1
и, следовательно, на этом шаге k-й шар окажется в мешке. Это произойдет до истечения минуты или в момент, сколь угодно близкий к ее окончанию. Таким образом, получается, что любой конкретный шар (с любым заданным номером) к моменту окончания минуты будет в мешке.
Зануда. Однако к этому же моменту, как мы убедились чуть ранее, вне мешка будут находиться бесконечно много шаров. Парадокс!
Профессор. Вы оба рассуждали довольно разумно, но упустили из виду важное обстоятельство, что и привело к противоречию. Обратите внимание, что алгоритм, состоящий из бесконечного количества извлечений-возвращений шаров, привязанных к моментам времени внутри минуты, не определен для последнего момента этой минуты. Данный алгоритм состоит из бесконечного количества шагов, но продолжительность его работы меньше одной минуты. Действительно, время работы алгоритма определяется суммой бесконечного количества временных интервалов между его шагами — 1/21 + 1/22 + 1/23 + … + 1/2n-1 + …. Для любого, сколь угодно большого числа шагов эта сумма меньше 1. Эту единицу можно рассматривать лишь как тот предел, к которому сумма постоянно приближается с добавлением каждого нового члена, но ни при каком конечном числе всех членов не достигает его. Последний момент минуты не принадлежит временному интервалу работы алгоритма, на котором он определен, а значит, мы не можем сказать, что он сотворит в этот момент.
Простак. Тем не менее мы можем предсказать, что будет в момент, сколь угодно близкий к концу минуты.
Профессор. Разумеется, поскольку для такого момента всегда найдется интервал, концы которого привязаны к двум смежным шагам алгоритма, содержащий этот момент.
Простак. Но как Вы объясните следующее обстоятельство. С одной стороны, алгоритм выполняет бесконечное количество шагов, т.е. никогда не завершает своей работы. С другой стороны, длительность его работы не может превысить одной минуты. Что же мы будем реально наблюдать в момент окончания минуты и далее? С одной стороны, спустя минуту и сколько угодно времени алгоритм должен продолжать работу, так как в противном случае он не содержал бы бесконечное количество шагов. Но, с другой стороны, он не определен на интервале времени, начинающемся с конца рассматриваемой минуты. Словом, я не могу представить себе эту противоречивую ситуацию.
Профессор. Противоречивую ситуацию всегда трудно себе представить наглядно, на то она и противоречивая. Поэтому математики и считают противоречивые объекты несуществующими.
Представьте себе некий алгоритм, который, согласно своему определению, что-то делает только по пятницам. А вас интересует, что он делает в остальные дни недели. Правомерно ли это? Думаю, что нет. Этот гипотетический алгоритм работает бесконечно долго, если считать, что время никогда не остановится и пятницы будут следовать друг за другом через каждую неделю. Однако для наблюдателя, переживающего сейчас, например, понедельник данный алгоритм просто ничего не делает, ожидая очередной пятницы. Если вы скажете, что такое ожидание входит в определение алгоритма и тем самым является его деятельностью, то тогда я скажу, что алгоритм приостановился на неделю.
